3 Delineamento em Blocos Casualizados
Caracterização
O delineamento em blocos casualizados (DBC) é o mais utilizado dos delineamentos experimentais, e os experimentos instalados de acordo com esse delineamento são denominados de experimentos em blocos casualizados ou experimentos em blocos ao acaso. Além dos princípios da repetição e da casualização, leva em conta também o princípio do controle local.
Sempre que houver dúvidas a respeito da homogeneidade das condições experimentais é conveniente usar o princípio do controle local, estabelecendo blocos com parcelas homogêneas.
As principais características deste delineamento são:
As parcelas são distribuídas em grupos ou blocos (princípio do controle local) de tal forma que elas sejam o mais uniforme possível dentro de cada bloco.
O número de parcelas por bloco deve ser igual ao número de tratamentos (blocos completos casualizados).
Os tratamentos são designados às parcelas de forma casual, sendo essa casualização feita dentro de cada bloco.
Esse delineamento é mais eficiente que o delineamento inteiramente casualizado, e essa eficiência depende da uniformidade das parcelas dentro de cada bloco, podendo inclusive, haver diferenças acentuadas de um bloco para outro.
Então, por exemplo, se temos um experimento em blocos casualizados em que desejamos estudar o efeito de 4 variedades (V1,V2,V3 e V4), sendo cada uma delas repetidas 5 vezes, teremos o seguinte plano experimental:
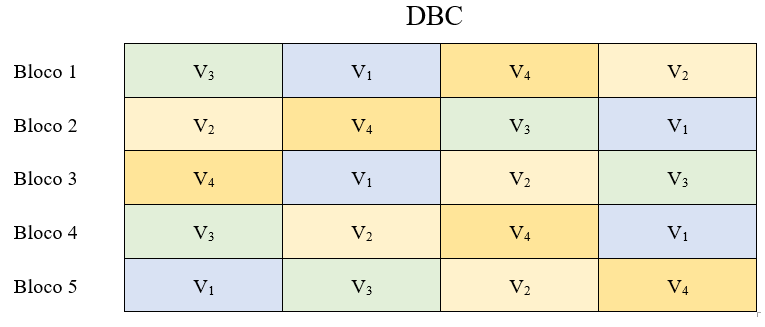
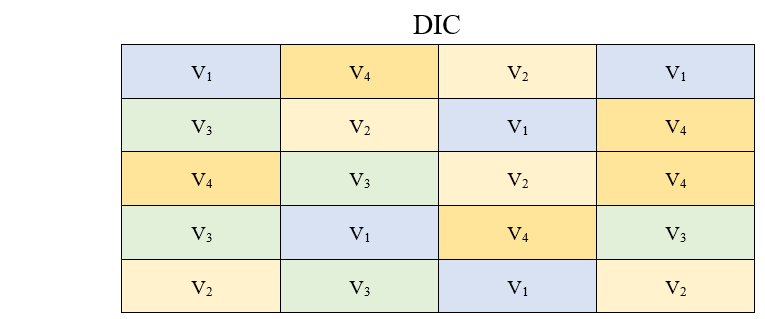
Note que dentro de cada bloco temos as variedades sorteadas ao acaso. Caso este mesmo ensaio fosse montado no delineamento inteiramente casualizados, o sorteio seria feito em todas as parcelas do experimento, e os tratamentos não seriam agrupados em blocos. Por exemplo, no delineamento inteiramente casualizado teríamos:
As principais vantagens desse delineamento são:
Controla as diferenças que ocorrem nas condições experimentais de um bloco para outro.
Permite, dentro de certos limites, utilizar qualquer número de tratamentos e blocos.
Nos conduz a uma estimativa mais exata para a variância residual.
A análise de variância é relativamente simples, sendo apenas um pouco mais demorada que a do delineamento inteiramente casualizado, pois possui uma causa de variação a mais (Blocos).
As principais desvantagens desse delineamento são:
Pela utilização do princípio do controle local há uma diminuição no número de graus de liberdade do resíduo.
A exigência de homogeneidade dentro do bloco limita o número de tratamentos, que não pode ser muito grande.
Modelo matemático
Para podermos analisar um experimento em qualquer delineamento, necessitamos conhecer o modelo matemático do mesmo, e aceitar algumas hipóteses básicas necessárias para a validade da análise de variância.
O modelo matemático do delineamento em blocos casualizados é o seguinte:
\[ x_{ij} = \mu +\tau_i + \beta_j+\epsilon_{ij} \]
onde, \(x_{ij}\) representa o valor esperado na parcela que recebeu o tratamento \(i\) e que se encontra no bloco \(j\).
\(\mu\) é a média geral do experimento.
\(\tau_i\) é o efeito devido ao tratamento i que foi aplicado à parcela.
\(\beta_j\) é o efeito devido ao bloco j em que se encontra a parcela.
\(\epsilon_{ij}\) é o efeito dos fatores não controlados ou acaso na parcela que recebeu o tratamento i e que se encontra no bloco j.
CRITÉRIO DO TESTE:
Para Tratamentos:
Comparamos o valor F calculado para tratamentos com o valor de F tabelado em função do número de GL de Tratamentos e GL do resíduo, ao nível \(\alpha\) de significância.
Se \(F_{Trat} > F_{Tab}\), concluímos que o teste é significativo, portanto, rejeitamos \(H_0\) e devemos concluir que existe diferença significativa entre os efeitos dos tratamentos testados em relação à variáveis (característica) em estudo.
Para Blocos:
Pra Blocos, a comparação é feita entre o valor de F calculado com o F tabelado em função do número de GL de Blocos e GL do resíduo, ao nível \(\alpha\) de significância
Se \(F_{Blocos} > F_{Tab}\), concluímos que o teste é significativo, portanto, rejeitamos \(H_0\) e devemos concluir que os blocos possuem efeitos diferentes em relação à característica em estudo, ou seja, os blocos foram eficientes no controle da heterogeneidade local.
Exemplo de aplicação do DBC
No trabalho “Influência do genótipo e da adubação sobre algumas características fenotípicas de Zea mays L (Milho),” realizado por BARBOSA (1976), foram utilizadas 4 cultivares de milho:
\(C_1\) = OPACO 2
\(C_2\) = PIRANÃO
\(C_3\) = COMPOSTO FLINT
\(C_4\) = AGROCERES AG-152
O ensaio foi montado de acordo com o delineamento em blocos casualizados, sendo utilizados 5 blocos para controlar as diferenças de fertilidade do solo entre terraços.
Os resultados obtidos para a produção em kg/ha, foram os seguintes e podem ser encontrados online em milho.
| Tratamentos | Bloco1 | Bloco2 | Bloco3 | Bloco4 | Bloco5 | Total |
|---|---|---|---|---|---|---|
| OPACO2 | 2812 | 2296 | 3501 | 3301 | 3691 | 15601 |
| PIRANAO | 3728 | 3588 | 4418 | 4544 | 5084 | 21362 |
| COMP.FLINT | 5359 | 5106 | 7477 | 8007 | 7956 | 33905 |
| AG152 | 4482 | 4510 | 5236 | 5930 | 5025 | 25183 |
| Total | 16381 | 15500 | 20632 | 21782 | 21756 | 96051 |
As hipóteses que desejamos testar são as seguintes:
\[ \begin{cases} H_0: As\;cultivares\;testadas\;não\;diferem\;entre\;si\;em\;relação\;à\;produção\;da\;cultura\;do\;milho. \\ H_1: As\;cultivares\;testadas\;diferem\;entre\;si\;em\;relação\;à\;produção\;da\;cultura\;do\;milho. \end{cases} \]
Aplicação em R - DBC

library(ExpDes.pt)caminho<-"https://raw.githubusercontent.com/arpanosso/curso_GIEU/master/dados/milho.txt"
dados<-read.table(caminho,h=T,sep="\t")
head(dados)## trat bloco y
## 1 OPACO2 1 2812
## 2 OPACO2 2 2296
## 3 OPACO2 3 3501
## 4 OPACO2 4 3301
## 5 OPACO2 5 3691
## 6 PIRANAO 1 3728# Extraindo os fatores e a variável resposta
trat<-as.factor(dados$trat)
bloco<-as.factor(dados$bloco)
y<-dados$y
# Definindo o modelo matemático
modelo<-aov(y~trat+bloco)
anova(modelo)## Analysis of Variance Table
##
## Response: y
## Df Sum Sq Mean Sq F value Pr(>F)
## trat 3 35402022 11800674 44.3450 9.068e-07 ***
## bloco 4 9221681 2305420 8.6634 0.00158 **
## Residuals 12 3193330 266111
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Utilizando o pacote “ExpDes.pt”
# Utilizando a função
dbc(trat,bloco,y, quali = TRUE, mcomp = "tukey")## ------------------------------------------------------------------------
## Quadro da analise de variancia
## ------------------------------------------------------------------------
## GL SQ QM Fc Pr>Fc
## Tratamento 3 35402022 11800674 44.345 0.00000091
## Bloco 4 9221681 2305420 8.663 0.00158020
## Residuo 12 3193330 266111
## Total 19 47817033 14372205
## ------------------------------------------------------------------------
## CV = 10.74 %
##
## ------------------------------------------------------------------------
## Teste de normalidade dos residuos
## valor-p: 0.1786606
## De acordo com o teste de Shapiro-Wilk a 5% de significancia, os residuos podem ser considerados normais.
## ------------------------------------------------------------------------
##
## ------------------------------------------------------------------------
## Teste de homogeneidade de variancia
## valor-p: 0.03461775
## ATENCAO: a 5% de significancia, as variancias nao podem ser consideradas homogeneas!
## ------------------------------------------------------------------------
##
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a COMP.FLINT 6781
## b AG152 5036.6
## b PIRANAO 4272.4
## c OPACO2 3120.2
## ------------------------------------------------------------------------