2 Delineamento Inteiramente Casualizado
Caracterização
O delineamento inteiramente casualizado é o mais simples de todos os delineamentos experimentais, e os experimentos instalados de acordo com este delineamento são chamado de experimentos inteiramente casualizados ou experimentos inteiramente ao acaso (DIC).
Este delineamento apresenta as seguintes características:
Leva em consideração os princípios da repetição e da casualização, deixando de lado o princípio do controle local e, portanto, as repetições não são organizadas em blocos.
Os tratamentos são designados às parcelas de forma inteiramente casual, com qualquer número de repetições.
As principais vantagens desse delineamento são as seguintes:
Flexibilidade, uma vez que o número de repetições pode variar de um tratamento para outro, sem causar sérios problemas na análise.
Proporciona o maior número de graus de liberdade possível para o resíduo.
As principais desvantagens desse delineamento são:
As parcelas experimentais devem ser homogêneas.
Leva a uma alta estimativa da variância residual \(QM_{Res}\), uma vez que todas as variações, exceto aquela devido ao efeito de tratamentos, são tomadas como variação do acaso.
Para a instalação desse experimento devemos ter certeza da homogeneidade das condições experimentais. Este delineamento é bastante utilizado em ensaios de laboratório e em ensaios com vasos, realizados dentro de casas de vegetação, em que as condições experimentais podem ser perfeitamente controladas.
A distribuição casual dos tratamentos a todas as parcelas do experimento é a principal característica deste delineamento. Por exemplo, num experimento no delineamento inteiramente casualizado com 5 tratamentos e 5 repetições, a casualização dos tratamentos seria feita sorteando-se para cada uma das 20 parcelas do experimento uma combinação de tratamento e repetição, ou seja:
\[ \begin{matrix} A1 & A2 & A3 & A4 \\ B1 & B2 & B3 & B4 \\ C1 & C2 & C3 & C4 \\ D1 & D2 & D3 & D4 \\ E1 & E2 & E3 & E4 \end{matrix} \]
Assim, um sorteio para distribuição dos tratamentos às parcelas poderia ser o seguinte:
\[ \begin{matrix} B4 & D1 & B1 & A2 & D4\\ D2 & A1 & C4 & D3 & B3\\ E1 & E3 & B2 & C2 & C2\\ A4 & C1 & E4 & E2 & E2 \end{matrix} \]
Modelo Matemático
Todo delineamento experimental possui um modelo matemático que o representa, que deve ser levado em conta na análise de variância, aceitando algumas hipóteses básicas necessárias para a validade da análise. No caso do DIC.
\[ x_{ij}= \mu + \tau_i + \epsilon_{ij} \] onde: \(x{ij}\): é o valor observado na parcela que recebeu o tratamento i na repetição j,
\(\mu\): é a média geral do experimento,
\(\tau_i\) é o efeito devido ao tratamento i que foi aplicado à parcela,
\(\epsilon_{ij}\) é o efeito dos fatores não controlados na parcela que recebeu o tratamento i na repetição j.
Hipóteses básicas para aplicação da análise de variância
As hipóteses básicas que devemos admitir para tornar válida a aplicação da análise de variância são as seguintes:
Aditividade: Os efeitos dos fatores do modelo são aditivos.
Independência: Os erros (desvios) \(\epsilon_{ij}\), devido aos efeitos de fatores não controlados ou acaso devem ser independentes.
Homocedasticidade (homogeneidade de variâncias): Os erros (desvios) \(\epsilon_{ij}\), devido ao acaso devem possuir variância comum \(\sigma^2\)
Normalidade dos desvios: Os erros ou desvios \(\epsilon_{ij}\) devido ao acaso devem possuir distribuição normal de probabilidades.
Uma forma resumida de apresentar estas quatro pressuposições é apresentada a seguir:
\[ \epsilon_{ij} \overset{iid}{\tilde{}} N(0,\sigma^2) \\ \]
Exemplo de aplicação DIC
Num experimento inteiramente casualizado, de competição de variedades de mandioca, realizado numa área perfeitamente homogênea quanto às condições experimentais, foram utilizadas 5 repetições das seguintes variedades:
1 - IAC 5
2 - IAC 7
3 - IAC 11
4 - IRACEMA
5 - MANTIQUEIRA
A designação dos tratamentos às parcelas no campo, juntamente com as produções, expressa em t/ha, foi a seguinte:
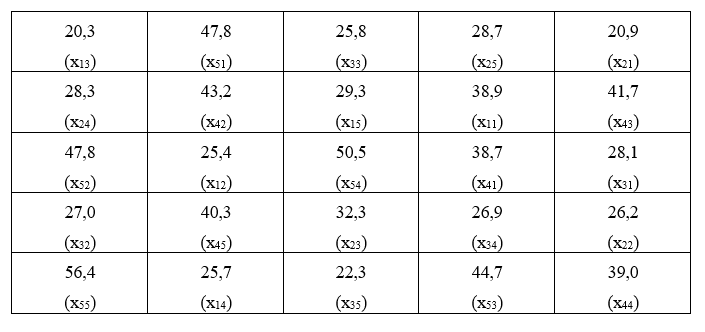
Com estes dados, podemos organizar o quadro seguinte:
| Tratamentos | Rep.1 | Rep.2 | Rep.3 | Rep.4 | Rep. 5 | Total |
|---|---|---|---|---|---|---|
| 1 - IAC 5 | 38,9 | 25,4 | 20,3 | 25,7 | 29,3 | 139,6 |
| 2 - IAC 7 | 20,9 | 26,2 | 32,3 | 28,3 | 28,7 | 136,4 |
| 3 - IAC 11 | 28,1 | 27,0 | 25,8 | 26,9 | 22,3 | 130,1 |
| 4 - IRACEMA | 38,7 | 43,2 | 41,7 | 39,0 | 40,3 | 202,9 |
| 5 - MANTIQUEIRA | 47,8 | 47,8 | 44,7 | 50,5 | 56,4 | 247,2 |
| Total | 856,2 |
As hipóteses que desejamos testar são:
\(H_0\): As variedades de mandioca testadas não são diferentes entre si quanto à produção.
\(H_1\): As variedades de mandioca testadas diferem entre si quanto à produção.
Aplicação no R - DIC
Utilizando o R para obtermos o quadro da análise de variância, os dados estão disponíveis online em: Mandioca.

# Carregando o pacote para a análise
library(ExpDes.pt)# Definindo o caminho dos dados
caminho<-"https://raw.githubusercontent.com/arpanosso/curso_GIEU/master/dados/mandioca.txt"
# Lendo o arquivo de dados
dados<-read.table(caminho, h=T, sep="\t")
# verificando os 6 primeiros registros
head(dados)## Trat Rep Y
## 1 1 1 38.9
## 2 1 2 25.4
## 3 1 3 20.3
## 4 1 4 25.7
## 5 1 5 29.3
## 6 2 1 20.9# Análise de variância e teste de Tukey com a função dic
trat <- as.factor(dados$Trat) # Criando o vetor de tratamentos
y <- dados$Y # Criando o vetor com a variável resposta
# Criando o modelo
mod <- aov(y ~ trat)
anova(mod)## Analysis of Variance Table
##
## Response: y
## Df Sum Sq Mean Sq F value Pr(>F)
## trat 4 2135.94 533.98 28.592 5.077e-08 ***
## Residuals 20 373.52 18.68
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# Utilizando a função dic - delineamento inteiramente casualizado
dic(trat, y, quali=TRUE, mcomp = "tukey")## ------------------------------------------------------------------------
## Quadro da analise de variancia
## ------------------------------------------------------------------------
## GL SQ QM Fc Pr>Fc
## Tratamento 4 2135.94 533.98 28.592 5.0773e-08
## Residuo 20 373.52 18.68
## Total 24 2509.46 552.66
## ------------------------------------------------------------------------
## CV = 12.62 %
##
## ------------------------------------------------------------------------
## Teste de normalidade dos residuos
## Valor-p: 0.2156065
## De acordo com o teste de Shapiro-Wilk a 5% de significancia, os residuos podem ser considerados normais.
## ------------------------------------------------------------------------
##
## ------------------------------------------------------------------------
## Teste de homogeneidade de variancia
## valor-p: 0.1115615
## De acordo com o teste de bartlett a 5% de significancia, as variancias podem ser consideradas homogeneas.
## ------------------------------------------------------------------------
##
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a 5 49.44
## b 4 40.58
## c 1 27.92
## c 2 27.28
## c 3 26.02
## ------------------------------------------------------------------------